Tabla de frecuencias, Medidas de centralización, Medidas de dispersión, Cuantiles, Diagramas

Estadística unidimensional

Tabla de frecuencias

Ejemplo de tabla de frecuencias con datos agrupados:

Datos de altura en cm de una muestra de 25 personas:

153, 172, 165, 176, 181, 168, 156, 164, 175, 179, 187, 150, 159, 165, 163, 174, 191, 181, 184, 175, 177, 179, 189, 161, 171

Se agrupan en intervalos de amplitud 10;
[150, 160), [160, 170), [170, 180), [180, 190), [190, 200)

Tabla de frecuencias

Intervalo	$M.C.={{\mathbf{x}}_{\mathbf{i}}}$	${{\mathbf{f}}_{\mathbf{i}}}$	${{\mathbf{F}}_{\mathbf{i}}}$	${\mathbf{f}}{{\mathbf{r}}_{\mathbf{i}}}$	${\mathbf{F}}{{\mathbf{r}}_{\mathbf{i}}}$	${{\mathbf{x}}_{\mathbf{i}}}\cdot{{\mathbf{f}}_{\mathbf{i}}}$	${\mathbf{x}}_i^2 \cdot{{\mathbf{f}}_{\mathbf{i}}}$	$\left\|{{{\mathbf{x}}_{\mathbf{i}}}-{\mathbf{\bar x}}}\right\| \cdot{{\mathbf{f}}_{\mathbf{i}}}$
$\begin{gathered}\left[{150,\;160}\right) \\ \left[{160,\;170}\right) \\ \left[{170,\;180}\right) \\ \left[{180,\;190}\right) \\ \left[{190,\;200}\right) \\ \end{gathered}$	$\begin{gathered}155 \\ 165 \\ 175 \\ 185 \\ 195 \\ \end{gathered}$	$\begin{gathered}4 \\ 6 \\ 9 \\ 5 \\ 1 \\ \end{gathered}$	$\begin{gathered}4 \\ 10 \\ 19 \\ 24 \\ 25 \\ \end{gathered}$	$\begin{gathered}16\% \\ 24\% \\ 36\% \\ 20\% \\ 4\% \\ \end{gathered}$	$\begin{gathered}16\% \\ 40\% \\ 76\% \\ 96\% \\ 100\% \\ \end{gathered}$	$\begin{gathered}620 \\ 990 \\ 1575 \\ 925 \\ 195 \\ \end{gathered}$	$\begin{gathered}\\ \\ \vdots \\ \\ \\ \end{gathered}$	$\begin{gathered}\\ \\ \vdots \\ \\ \\ \end{gathered}$
		$\sum{{{\mathbf{f}}_{\mathbf{i}}}}=N$				$\sum{{{\mathbf{x}}_{\mathbf{i}}}\cdot{{\mathbf{f}}_{\mathbf{i}}}}$	$\sum{{\mathbf{x}}_i^2 \cdot{{\mathbf{f}}_{\mathbf{i}}}}$	$\sum{\left\|{{{\mathbf{x}}_{\mathbf{i}}}-{\mathbf{\bar x}}}\right\|}\cdot{{\mathbf{f}}_{\mathbf{i}}}$

${L_i}$ : límite inferior del intervalo considerado
${L_s}$ : límite superior del intervalo considerado
Marca de clase o valor representativo del intervalo, es la media aritmética del intevalo: $M.C.={{\mathbf{x}}_{\mathbf{i}}}=\frac{{{L_i}+{L_s}}}{2}$
Frecuencia absoluta ${{\mathbf{f}}_{\mathbf{i}}}$ : Número de veces que se repite un dato
Frecuencia total $\sum{{{\mathbf{f}}_{\mathbf{i}}}}=N$ : Número total de datos. Es igual a la suma de todas las frecuencias absolutas
Frecuencia acumulada ${{\mathbf{F}}_{\mathbf{i}}}$ : Suma de frecuencia absoluta del dato i mas las frecuencias absolutas de los datos anteriores
Frecuencia relativa ${\mathbf{f}}{{\mathbf{r}}_{\mathbf{i}}}$ : Cociente entre la frecuencia absoluta del dato i y el número total de datos
Frecuencia acumulada relativa ${\mathbf{F}}{{\mathbf{r}}_{\mathbf{i}}}$ : Suma de la frecuencia relativa del dato i con las frecuencias relativas de todos los datos anteriores

Medidas de centralización

Media:

\bar x=\frac{{\sum{{x_i}\cdot{f_i}}}}{N}

Moda: Es el dato que más se repite

Datos sin agrupar: Se toma el valor con mayor frecuencia absoluta
Datos agrupados. Sobre el intervalo modal (de mayor frecuencia absoluta): $Mo={L_i}+ c \cdot \frac{{{D_1}}}{{{D_1}+{D_2}}}$

Mediana: Es el valor que ocupa la posición central de la lista ordenada

Datos sin agrupar: Se toma el valor con mayor frecuencia absoluta
- Si N impar: $Me={x_{\frac{{N + 1}}{2}}}$
- Si N par: $Me=\frac{{{x_{\frac{N}{2}}}+{x_{\frac{N}{2}+ 1}}}}{2}$
Datos agrupados: Sobre el intervalo mediano (aquel donde ${F_i}\geqslant \frac{N}{2}$ ): $Me={L_i}+ c \cdot \frac{{\frac{N}{2}-{F_{i - 1}}}}{{{f_i}}}$

${L_i}$ : límite inferior del intervalo considerado
${c}$ : Amplitud del intervalo (Diferencia entre el valor superior e inferior)
${D_1}={f_i}-{f_{i - 1}}$ : Diferencia entre la frecuencia absoluta del intervalo modal y del intervalo anterior
${D_2}={f_i}-{f_{i + 1}}$ : Diferencia entre la frecuencia absoluta del intervalo modal y del intervalo posterior
${x_{\frac{{N + 1}}{2}}}$ : Valor en la posición $\frac{{N + 1}}{2}$
${x_{\frac{N}{2}}}$ : Valor en la posición $\frac{N}{2}$
${x_{\frac{N}{2}+ 1}}$ : Valor en la posición $\frac{N}{2}+ 1$
${F_i}$ : Frecuencia absoluta acumulada del intervalo mediano
${f_i}$ : Frecuencia absoluta del intervalo mediano

Medidas de dispersión

Rango:

{x_{\max}}-{x_{\min}}

Desviación media: respecto a la media

{D_{\bar x}}=\frac{{\sum{\left|{{x_i}- \bar x}\right| \cdot{f_i}}}}{N}

Varianza:

{\sigma ^2}=\frac{{\sum{x_i^2 \cdot{f_i}}}}{N}-{\bar x^2}

Desviación típica:

\sigma=\sqrt{\frac{{\sum{x_i^2 \cdot{f_i}}}}{N}-{{\bar x}^2}}

Coeficiente de variación:

C.V=\frac{\sigma}{{\bar x}}

Cuantiles

Son valores de variable estadística que dividen a la distribución en intervalos con igual número de datos cada uno de ellos

Cuartiles: Son tres valores (Q1 , Q2 , Q3 ) que determinan las posiciones correspondientes al 25%, al 50% y al 75% de los datos, dividiendo la distribución en cuatro subconjuntos con el 25% de los datos cada uno de ellos. La diferencia entre los cuartiles superior e inferior se llama rango intercuartílico
Quintiles: Son cuatro valores(K1 , K2 , K3 , K4 ) que determinan las posiciones correspondientes al 20%, 40%, 60%, y 80% de los datos, dividiendo la distribución en cinco subconjuntos con el 20% de los datos cada uno de ellos
Deciles: Son nueve valores (D1 , D2 ,..., D9) que corresponden al 10%, 20%,..., y 90% de los datos. Dividen a la distribución en diez subconjuntos con el 10% de los datos cada uno de ellos
Percentiles (o centiles): Son noventa y nueve valores (P1 , P2 , ...P99 ) que dan el valor de la posición correspondiente a cualquier porcentaje. Dividen a la distribución en cien subconjuntos

Datos sin agrupar: Se busca el primer valor que cumpla:

{F_i}\geqslant k \cdot \frac{N}{n}

Datos agrupados: Se busca el intervalo donde se encuentra el cuantil deseado, y sobre este intervalo se hace una interpolación mediante la expresión

{n_k}={L_i}+ c \cdot \frac{{k \cdot \frac{N}{n}-{F_{i - 1}}}}{{{f_i}}}

n: indica el tipo de cuantil;
- Para cuartiles n=4
- Para quintiles n=5
- Para deciles n=10
- Para percentiles n=100
k: Especifica el cuantil buscado

N: Tamaño de la muestra
${L_i}$ : Límite inferior del intervalo
c: Amplitud del intervalo
${F_i}$ : Frecuencia absoluta acumulada del intervalo
${f_i}$ : Frecuencia absoluta del intervalo

Ejemplos de cuantiles

1º Cuartil: Se divide la distribución en 4 tramos y se coge el 1º

{Q_1}={L_i}+ c \cdot \frac{{1 \cdot \frac{N}{4}-{F_{i - 1}}}}{{{f_i}}}

2º Cuartil: Corresponde a la mediana

{Q_2}={L_i}+ c \cdot \frac{{2\frac{N}{4}-{F_{i - 1}}}}{{{f_i}}}

7º Decil: Corresponde al 70% de los datos de la distribución

{D_7}={L_i}+ c \cdot \frac{{7\frac{N}{{10}}-{F_{i - 1}}}}{{{f_i}}}

2º Quintil: Se divide la distribución en 5 tramos y se coge el 2

{K_2}={L_i}+ c \cdot \frac{{2\frac{N}{5}-{F_{i - 1}}}}{{{f_i}}}

Percentil 35: Valor en la posición 35% de la distribución

{P_{35}}={L_i}+ c \cdot \frac{{35\frac{N}{{100}}-{F_{i - 1}}}}{{{f_i}}}

Diagramas

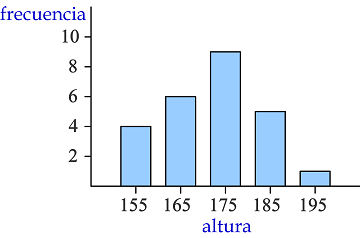
Gráfico de barras: Se representan los intervalos en el eje de abscisas con barras de igual ancho. La frecuencia se representa en el eje de ordenadas

Polígono de frecuencias: Es similar al anterior. Se representan los puntos, y se unen con segmentos Es útil para mostrar la tendencia de la variable estudiada

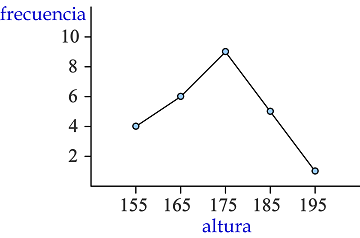
Gráfico de cajas y bigotes: Estos gráficos sintetizan la información de una distribución partiéndola en cuatro partes. Los puntos de división son los cuatro cuartiles
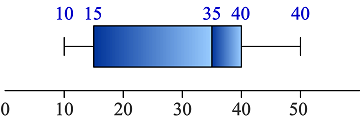
Ejemplo: Sea un conjunto de datos cuyos cuartiles son; C1=15, C2=35, C3=40. El mayor y menor dato son 10 y 50 respectivamente